🎯要点
🎯达朗贝尔一维波动通解,二维变速模拟 | 🎯达朗贝尔算子解双曲波形微分方程 | 🎯耗散系统粘性伯格斯方程快速傅里叶变换算法 | 🎯二维线性和非线性对流扩散解和湍流隐式建模
📜偏微分方程用例:Python自动造波器椭圆曲线波孤子解
📜有限差分用例:Python微磁学磁倾斜和西塔规则算法


🍇Python一维粘性伯格斯方程
一维空间中粘性伯格斯方程的一般形式是耗散系统:
∂
u
∂
t
+
u
∂
u
∂
x
=
ν
∂
2
u
∂
x
2
\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=\nu \frac{\partial^2 u}{\partial x^2}
∂t∂u+u∂x∂u=ν∂x2∂2u
此项
u
∂
u
/
∂
x
u \partial u / \partial x
u∂u/∂x 也可以重写为
∂
(
u
2
/
2
)
/
∂
x
\partial\left(u^2 / 2\right) / \partial x
∂(u2/2)/∂x。当扩散项不存在时(即
ν
=
0
\nu=0
ν=0 ),粘性伯格斯程变为无粘伯格斯方程:
∂
u
∂
t
+
u
∂
u
∂
x
=
0
\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=0
∂t∂u+u∂x∂u=0
这是可以产生不连续性(冲击波)的守恒方程的原型。
当人们检查等式的左侧时, ν \nu ν 的小值形成锐梯度的原因就变得直观清楚了。此项 ∂ / ∂ t + u ∂ / ∂ x \partial / \partial t+u \partial / \partial x ∂/∂t+u∂/∂x 显然是一个波算子,描述以 u u u 速度沿正 x x x 方向传播的波。由于波速为 u u u,表现出较大 u u u值的区域将比表现出较小 u u u值的区域更快地向右传播;换句话说,如果 u u u 最初沿 x x x 方向减小,则位于背面的较大 u u u 将赶上位于正面的较小 u u u 。右侧扩散项的作用本质上是阻止梯度变得无穷大。
在此,我们将使用非线性对流和扩散,仅创建一维伯格方程。
∂
u
∂
t
+
u
∂
u
∂
x
=
ν
∂
2
u
∂
x
2
\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=\nu \frac{\partial^2 u}{\partial x^2}
∂t∂u+u∂x∂u=ν∂x2∂2u
我们可以离散化这个微分,采用以下形式:
u
i
n
+
1
−
u
i
n
Δ
t
+
u
i
n
u
i
n
−
u
i
−
1
n
Δ
x
=
v
u
i
+
1
n
−
2
u
i
n
+
u
i
−
1
n
Δ
x
2
\frac{u_i^{n+1}-u_i^n}{\Delta t}+u_i^n \frac{u_i^n-u_{i-1}^n}{\Delta x}=v \frac{u_{i+1}^n-2 u_i^n+u_{i-1}^n}{\Delta x^2}
Δtuin+1−uin+uinΔxuin−ui−1n=vΔx2ui+1n−2uin+ui−1n
在解决了未知数之后,我们得到了用 Python 编码的算法。
u
i
n
+
1
=
u
i
n
−
u
i
n
Δ
t
Δ
x
(
u
i
n
−
u
i
−
1
n
)
+
v
Δ
t
Δ
x
2
(
u
i
+
1
n
−
2
u
i
n
+
u
i
−
1
n
)
u_i^{n+1}=u_i^n-u_i^n \frac{\Delta t}{\Delta x}\left(u_i^n-u_{i-1}^n\right)+v \frac{\Delta t}{\Delta x^2}\left(u_{i+1}^n-2 u_i^n+u_{i-1}^n\right)
uin+1=uin−uinΔxΔt(uin−ui−1n)+vΔx2Δt(ui+1n−2uin+ui−1n)
速度的初始条件是使用以下函数创建的:
u
=
−
2
v
ϕ
∂
ϕ
∂
x
+
4
ϕ
=
exp
(
−
x
2
4
v
)
+
exp
(
−
(
x
−
2
π
)
2
4
v
)
\begin{aligned} u & =-\frac{2 v}{\phi} \frac{\partial \phi}{\partial x }+4 \\ \phi & =\exp \left(\frac{- x ^2}{4 v}\right)+\exp \left(\frac{-( x -2 \pi)^2}{4 v}\right) \end{aligned}
uϕ=−ϕ2v∂x∂ϕ+4=exp(4v−x2)+exp(4v−(x−2π)2)
边界条件意味着周期性,由下式给出:
u
(
0
)
=
u
(
2
π
)
u(0)=u(2 \pi)
u(0)=u(2π)
有一个解析解:
u
=
−
2
v
ϕ
∂
ϕ
∂
x
+
4
ϕ
=
exp
(
−
(
x
−
4
t
)
2
4
v
(
t
+
1
)
)
+
exp
(
−
(
x
−
4
t
−
2
π
)
2
4
v
(
t
+
1
)
)
\begin{aligned} & u =-\frac{2 v}{\phi} \frac{\partial \phi}{\partial x }+4 \\ & \phi=\exp \left(\frac{-( x -4 t )^2}{4 v( t +1)}\right)+\exp \left(\frac{-( x -4 t -2 \pi)^2}{4 v( t +1)}\right) \end{aligned}
u=−ϕ2v∂x∂ϕ+4ϕ=exp(4v(t+1)−(x−4t)2)+exp(4v(t+1)−(x−4t−2π)2)
解该问题的Python代码如下:
import numpy as np
import sympy as sp
import pylab as pl
pl.ion()
x, nu, t = sp.symbols('x nu t')
phi = sp.exp(-(x-4*t)**2/(4*nu*(t+1))) + sp.exp(-(x-4*t-2*np.pi)**2/(4*nu*(t+1)))
phiprime = phi.diff(x)
u = -2*nu*(phiprime/phi)+4
from sympy.utilities.lambdify import lambdify
ufunc = lambdify ((t, x, nu), u)
nx = 101
nt = 100
dx = 2*np.pi/(nx-1)
nu = 0.07
dt = dx*nu
T = nt*dt
grid = np.linspace(0, 2*np.pi, nx)
un = np.empty(nx)
t = 0
u = np.asarray([ufunc(t, x, nu) for x in grid])
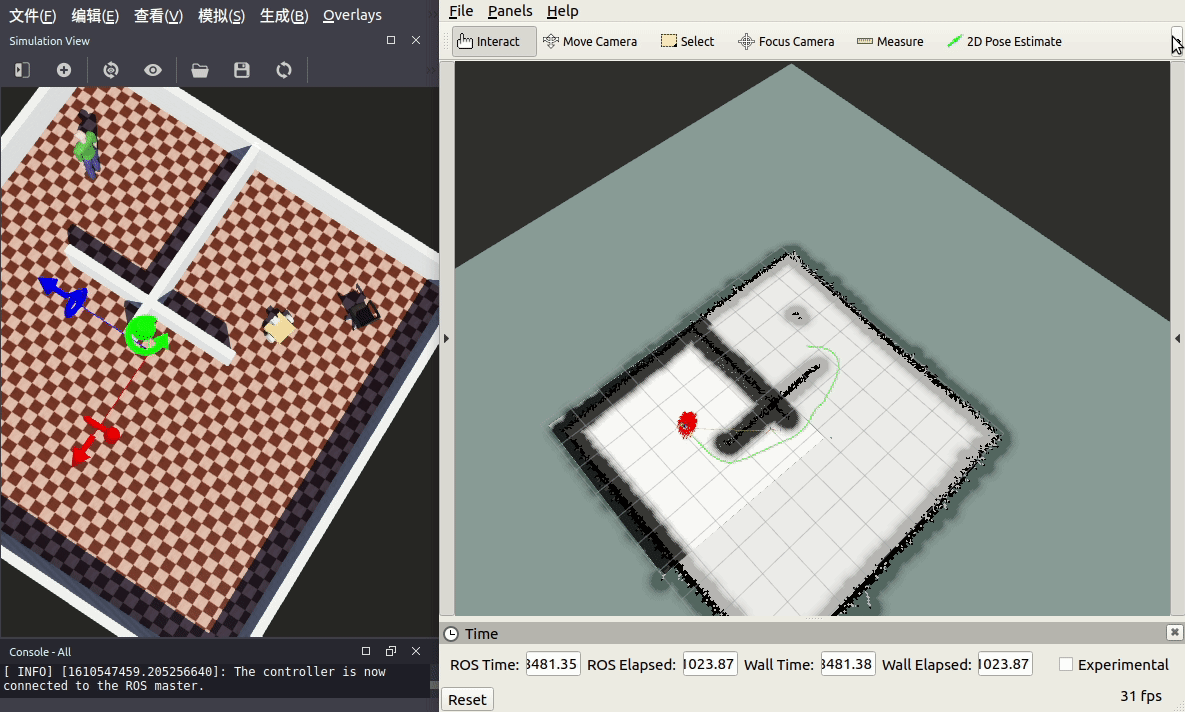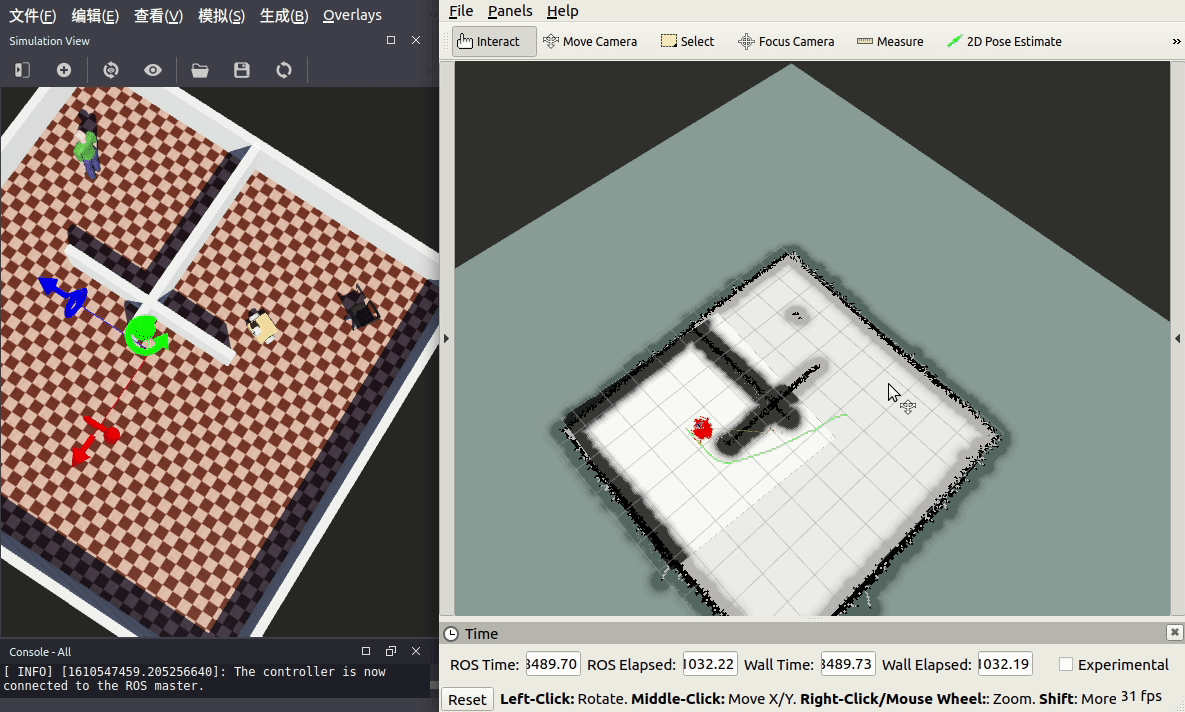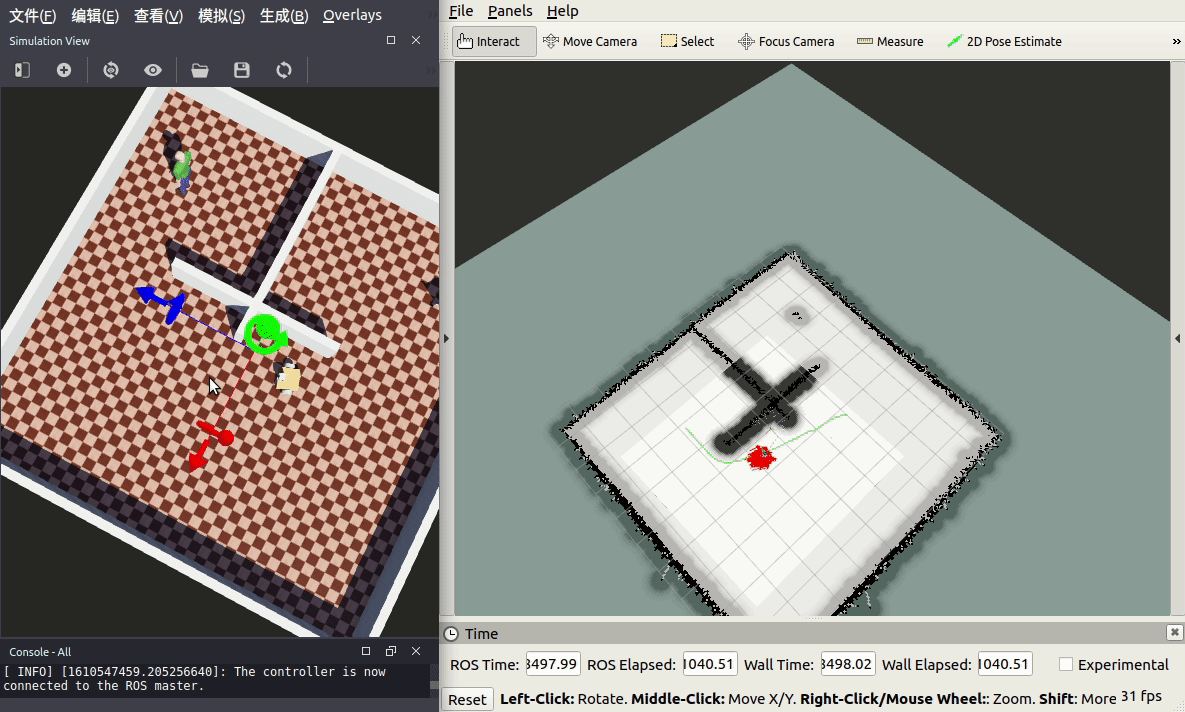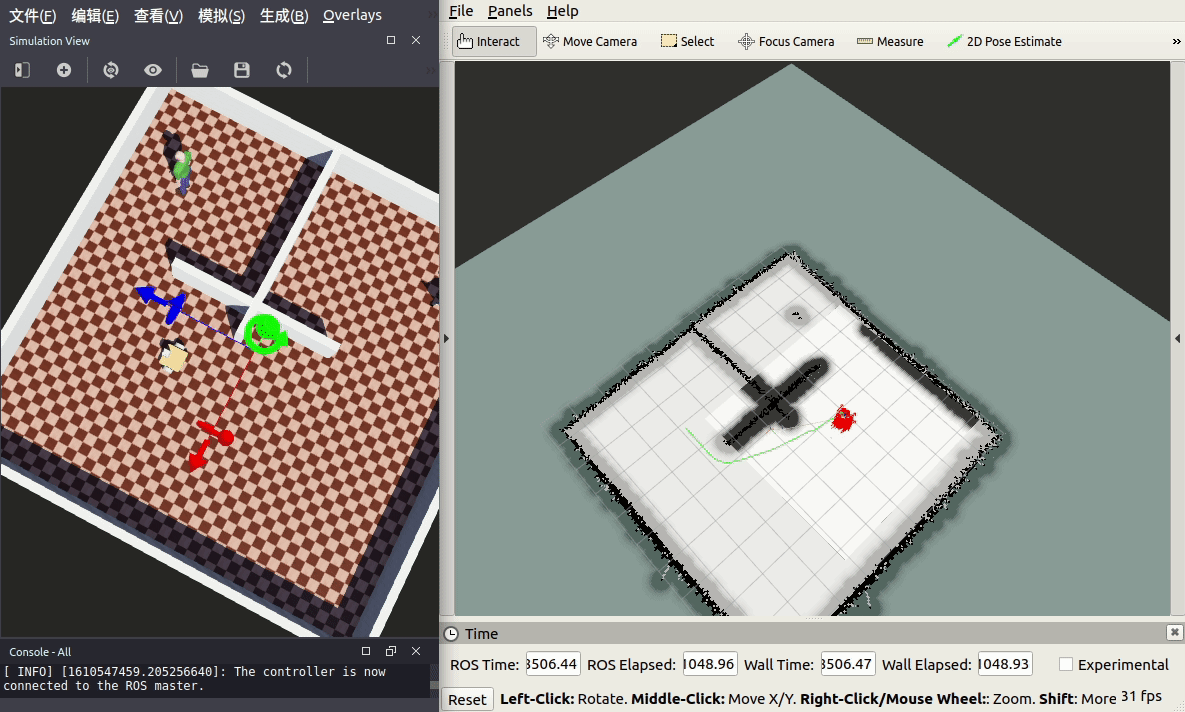
pl.figure(figsize=(11,7), dpi=100)
pl.plot(grid,u, marker='o', lw=2)
pl.xlim([0,2*np.pi])
pl.ylim([0,10])
pl.xlabel('X')
pl.ylabel('Velocity')
pl.title('1D Burgers Equation - Initial condition')
for n in range(nt):
un = u.copy()
for i in range(nx-1):
u[i] = un[i] - un[i] * dt/dx * (un[i]-un[i-1]) + \
nu * dt/(dx**2) * (un[i+1] - 2*un[i] + un[i-1])
u[-1] = un[-1] - un[-1] * dt/dx * (un[-1]-un[-2]) + \
nu * dt/(dx**2) * (un[0] - 2*un[-1] + un[-2])
u_analytical = np.asarray([ufunc(T, xi, nu) for xi in grid])
pl.figure(figsize=(11,7), dpi=100)
pl.plot(grid, u, marker='o', lw=2, label='Computational')
pl.plot(grid, u_analytical, label='Analytical')
pl.xlim([0, 2*np.pi])
pl.ylim([0,10])
pl.legend()
pl.xlabel('X')
pl.ylabel('Velocity')
pl.title('1D Burgers Equation - Solutions')









![[数据集][目标检测]游泳者溺水检测数据集VOC+YOLO格式4599张2类别](https://i-blog.csdnimg.cn/direct/94c6196f9c4c4ac3b3b315b68c7ae6b1.png)